
八种常见算法排序(一)
八种常见算法排序(一)
1. 插入排序
算法步骤:
将第一待排序序列第一个元素看做一个有序序列,把第二个元素到最后一个元素当成是未排序序列。从头到尾依次扫描未排序序列,将扫描到的每个元素插入有序序列的适当位置。(如果待插入的元素与有序序列中的某个元素相等,则将待插入元素插入到相等元素的后面。)
动图演示:

代码实现:
// 从下标为1的元素开始选择合适的位置插入,因为下标为0的只有一个元素,默认是有序的
for (int i = 1; i < arr.length; i++) {
// 记录要插入的数据
int tmp = arr[i];
// 从已经排序的序列最右边的开始比较,找到比其小的数
int j = i;
while (j > 0 && tmp < arr[j - 1]) {
arr[j] = arr[j - 1];
j--;
}
// 存在比其小的数,插入
if (j != i) {
arr[j] = tmp;
}
}
2. 希尔排序
算法步骤:
-
选择一个增量序列 t1,t2,……,tk,其中 ti > tj, tk = 1;
-
按增量序列个数 k,对序列进行 k 趟排序;
-
每趟排序,根据对应的增量 ti,将待排序列分割成若干长度为 m 的子序列,分别对各子表进行直接插入排序。仅增量因子为 1 时,整个序列作为一个表来处理,表长度即为整个序列的长度。
动图演示:
代码实现:
int length = arr.length;
int temp;
for (int step = length / 2; step >= 1; step /= 2) {
for (int i = step; i < length; i++) {
temp = arr[i];
int j = i - step;
while (j >= 0 && arr[j] > temp) {
arr[j + step] = arr[j];
j -= step;
}
arr[j + step] = temp;
}
}
3. 选择排序
算法步骤:
-
首先在未排序序列中找到最小(大)元素,存放到排序序列的起始位置。
-
再从剩余未排序元素中继续寻找最小(大)元素,然后放到已排序序列的末尾。
-
重复第二步,直到所有元素均排序完毕。
动图演示:

代码实现:
// 总共要经过 N-1 轮比较
for (int i = 0; i < arr.length - 1; i++) {
int min = i;
// 每轮需要比较的次数 N-i
for (int j = i + 1; j < arr.length; j++) {
if (arr[j] < arr[min]) {
// 记录目前能找到的最小值元素的下标
min = j;
}
}
// 将找到的最小值和i位置所在的值进行交换
if (i != min) {
int tmp = arr[i];
arr[i] = arr[min];
arr[min] = tmp;
}
}
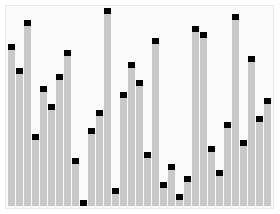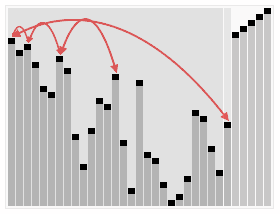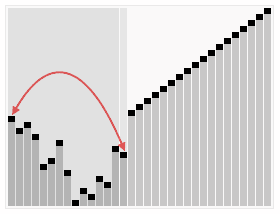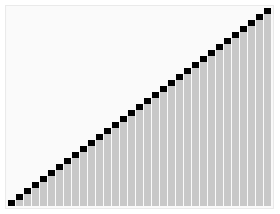
4. 堆排序
算法步骤:
- 创建一个堆 H[0……n-1];
- 把堆首(最大值)和堆尾互换;
- 把堆的尺寸缩小 1,并调用 shift_down(0),目的是把新的数组顶端数据调整到相应位置;
- 重复步骤 2,直到堆的尺寸为 1。
动图演示:
代码实现:
int len = arr.length;
buildMaxHeap(arr, len);
for (int i = len - 1; i > 0; i--) {
swap(arr, 0, i);
len--;
heapify(arr, 0, len);
}
return arr;
}
private void buildMaxHeap(int[] arr, int len) {
for (int i = (int) Math.floor(len / 2); i >= 0; i--) {
heapify(arr, i, len);
}
}
private void heapify(int[] arr, int i, int len) {
int left = 2 * i + 1;
int right = 2 * i + 2;
int largest = i;
if (left < len && arr[left] > arr[largest]) {
largest = left;
}
if (right < len && arr[right] > arr[largest]) {
largest = right;
}
if (largest != i) {
swap(arr, i, largest);
heapify(arr, largest, len);
}
}
private void swap(int[] arr, int i, int j) {
int temp = arr[i];
arr[i] = arr[j];
arr[j] = temp;
}
总结:
| 排序算法 | 时间复杂度(平均) | 时间复杂度(最坏) | 时间复杂度(最好) | 空间复杂度 | 稳定性 |
|---|---|---|---|---|---|
| 插入排序 | O(N^2) | O(N^2) | O(N) | O(1) | 稳定 |
| 希尔排序 | O(N^1.3) | O(N^2) | O(N) | O(1) | 不稳定 |
| 选择排序 | O(N^2) | O(N^2) | O(N^2) | O(1) | 不稳定 |
| 堆排序 | O(N*log2(N)) | O(N*log2(N)) | O(N*log2(N)) | O(1) | 不稳定 |
| 冒泡排序 | O(N^2) | O(N^2) | O(N) | O(1) | 稳定 |
| 快速排序 | O(N*log2(N)) | O(N^2) | O(N*log2(N)) | O(N*log2(N)) | 不稳定 |
| 归并排序 | O(N*log2(N)) | O(N*log2(N)) | O(N*log2(N)) | O(N) | 稳定 |
| 计数排序 | O(N+K) | O(N+K) | O(N+K) | O(N+K) | 稳定 |
本文是原创文章,采用 CC BY-NC-ND 4.0 协议,完整转载请注明来自 程序员小航
评论
匿名评论
隐私政策
你无需删除空行,直接评论以获取最佳展示效果
