
八种常见算法排序(二)
八种常见算法排序(二)
5. 冒泡排序
算法步骤:
- 比较相邻的元素。如果第一个比第二个大,就交换他们两个。
- 对每一对相邻元素作同样的工作,从开始第一对到结尾的最后一对。这步做完后,最后的元素会是最大的数。
- 针对所有的元素重复以上的步骤,除了最后一个。
- 持续每次对越来越少的元素重复上面的步骤,直到没有任何一对数字需要比较。
动图演示:

代码实现:
for (int i = 1; i < arr.length; i++) {
boolean flag = true;
for (int j = 0; j < arr.length-1-i; j++) {
if (arr[j] > arr[j+1]){
int temp = arr[j];
arr[j]=arr[j+1];
arr[j+1]=temp;
}
}
if (flag) {
break;
}
}
6. 快速排序
算法步骤:
- 从数列中挑出一个元素,称为 "基准"(pivot);
- 重新排序数列,所有元素比基准值小的摆放在基准前面,所有元素比基准值大的摆在基准的后面(相同的数可以到任一边)。在这个分区退出之后,该基准就处于数列的中间位置。这个称为分区(partition)操作;
- 递归地(recursive)把小于基准值元素的子数列和大于基准值元素的子数列排序;
动图演示:
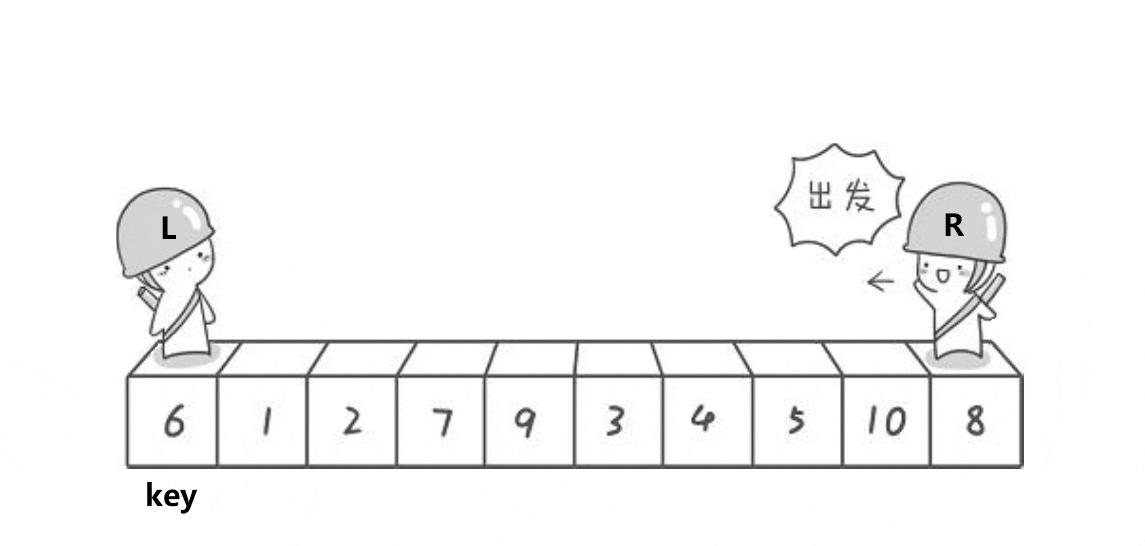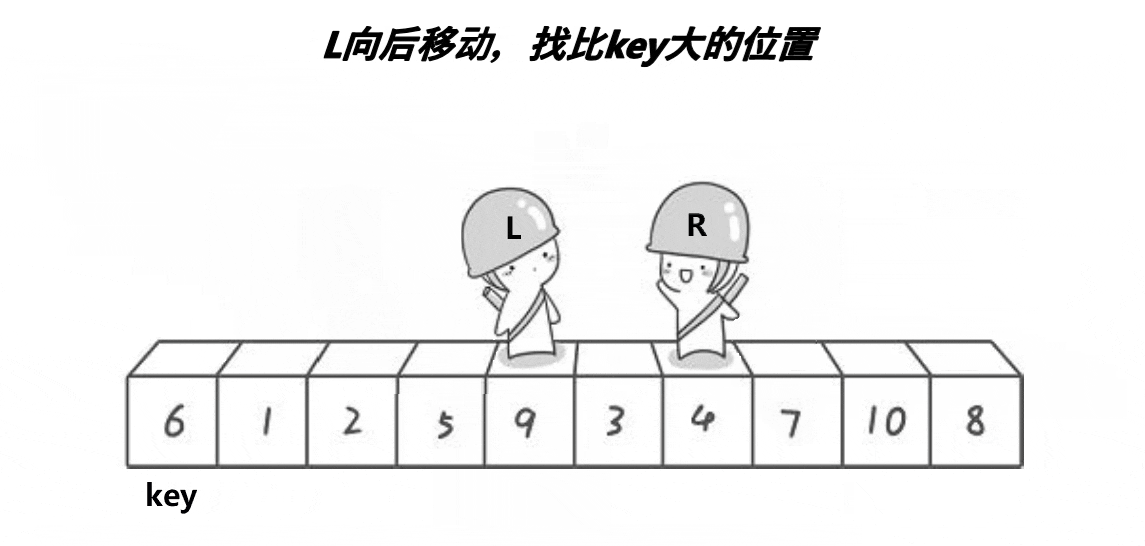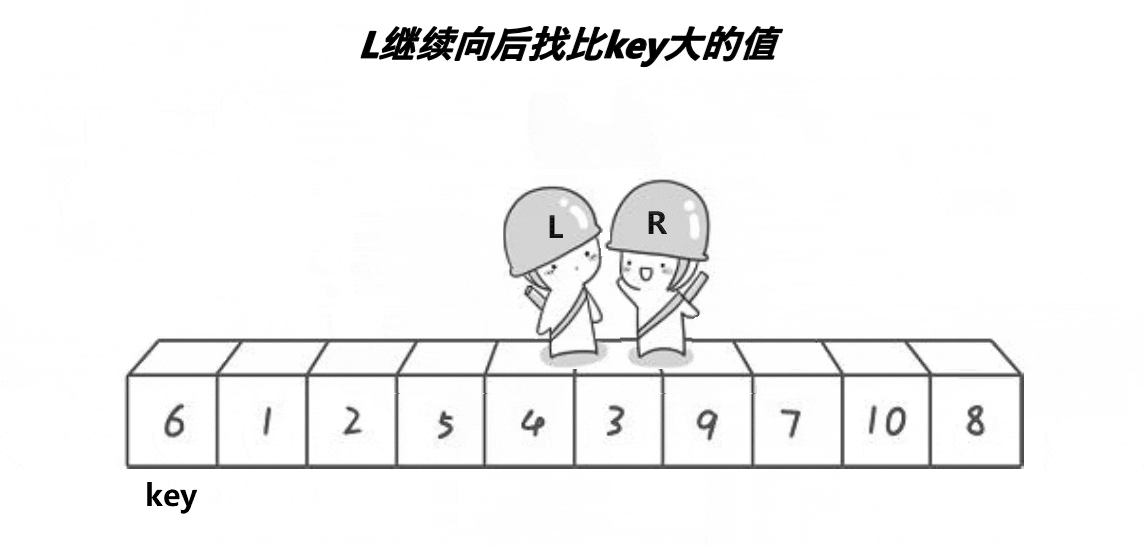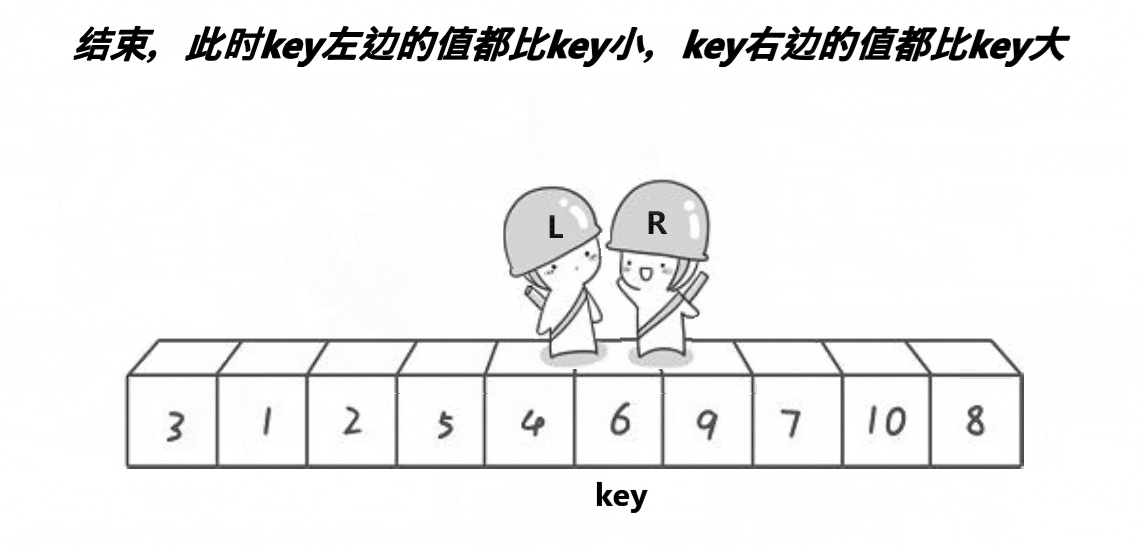
代码实现:
public static void quickSort(int[] arr,int left,int right) {
if (left > right) {
return;
}
int base = arr[left];
int i = left;
int j = right;
while (i != j) {
while (base <= arr[j] && j > i) {
j--;
}
while (base >= arr[i] && j > i) {
i++;
}
int temp = arr[i];
arr[i] = arr[j];
arr[j] = temp;
}
arr[left] = arr[i];
arr[i] = base;
quickSort(arr, left, i-1);
quickSort(arr, j+1, right);
}
7. 归并排序
**算法步骤:**申请空间,使其大小为两个已经排序序列之和,该空间用来存放合并后的序列;
- 设定两个指针,最初位置分别为两个已经排序序列的起始位置;
- 比较两个指针所指向的元素,选择相对小的元素放入到合并空间,并移动指针到下一位置;
- 重复步骤 3 直到某一指针达到序列尾;
- 将另一序列剩下的所有元素直接复制到合并序列尾。
动图演示:

代码实现:
public static void main (){
if (arr.length < 2) {
return arr;
}
int middle = (int) Math.floor(arr.length / 2);
int[] left = Arrays.copyOfRange(arr, 0, middle);
int[] right = Arrays.copyOfRange(arr, middle, arr.length);
int[] sortArr = merge(sort(left), sort(right));
}
protected int[] merge(int[] left, int[] right) {
int[] result = new int[left.length + right.length];
int i = 0;
while (left.length > 0 && right.length > 0) {
if (left[0] <= right[0]) {
result[i++] = left[0];
left = Arrays.copyOfRange(left, 1, left.length);
} else {
result[i++] = right[0];
right = Arrays.copyOfRange(right, 1, right.length);
}
}
while (left.length > 0) {
result[i++] = left[0];
left = Arrays.copyOfRange(left, 1, left.length);
}
while (right.length > 0) {
result[i++] = right[0];
right = Arrays.copyOfRange(right, 1, right.length);
}
return result;
}
8. 计数排序
算法步骤:
- 找出待排序的数组中最大和最小的元素
- 统计数组中每个值为i的元素出现的次数,存入数组C的第i项
- 对所有的计数累加(从C中的第一个元素开始,每一项和前一项相加)
- 反向填充目标数组:将每个元素i放在新数组的第C(i)项,每放一个元素就将C(i)减去1
动图演示:

代码实现:
public static void main (){
int maxValue = getMaxValue(arr);
int[] sortArr = countingSort(arr, maxValue);
}
private int[] countingSort(int[] arr, int maxValue) {
int bucketLen = maxValue + 1;
int[] bucket = new int[bucketLen];
for (int value : arr) {
bucket[value]++;
}
int sortedIndex = 0;
for (int j = 0; j < bucketLen; j++) {
while (bucket[j] > 0) {
arr[sortedIndex++] = j;
bucket[j]--;
}
}
return arr;
}
private int getMaxValue(int[] arr) {
int maxValue = arr[0];
for (int value : arr) {
if (maxValue < value) {
maxValue = value;
}
}
return maxValue;
}
总结:
| 排序算法 | 时间复杂度(平均) | 时间复杂度(最坏) | 时间复杂度(最好) | 空间复杂度 | 稳定性 |
|---|---|---|---|---|---|
| 插入排序 | O(N^2) | O(N^2) | O(N) | O(1) | 稳定 |
| 希尔排序 | O(N^1.3) | O(N^2) | O(N) | O(1) | 不稳定 |
| 选择排序 | O(N^2) | O(N^2) | O(N^2) | O(1) | 不稳定 |
| 堆排序 | O(N*log2(N)) | O(N*log2(N)) | O(N*log2(N)) | O(1) | 不稳定 |
| 冒泡排序 | O(N^2) | O(N^2) | O(N) | O(1) | 稳定 |
| 快速排序 | O(N*log2(N)) | O(N^2) | O(N*log2(N)) | O(N*log2(N)) | 不稳定 |
| 归并排序 | O(N*log2(N)) | O(N*log2(N)) | O(N*log2(N)) | O(N) | 稳定 |
| 计数排序 | O(N+K) | O(N+K) | O(N+K) | O(N+K) | 稳定 |
本文是原创文章,采用 CC BY-NC-ND 4.0 协议,完整转载请注明来自 程序员小航
评论
匿名评论
隐私政策
你无需删除空行,直接评论以获取最佳展示效果
